La legge di Moore è inesorabilmente vera: la potenza di calcolo di un computer raddoppia una volta ogni due anni, ma lo stesso Moore ha recentemente precisato che questa progressione si fermerà nei prossimi 10 anni a meno di un salto computazionale quantistico. Già sul finire degli anni ‘80 questo scenario fu entusiasticamente confermato dallo sviluppo di alcuni progetti di ricerca internazionali in ambito supercalcolo che coinvolsero l’Italia. In particolare, dal 1989 al 1993 prima e dopo la guerra del Golfo, l’Italia fu protagonista di un progetto di ricerca avanzato, del quale ebbi il privilegio di far parte. L’attività fu condotta a Roma e specularmente ad Orlando in California dal gruppo americano Bell Atlantic (con la controllata californiana BA Video Service) in partnership con il gruppo italiano a partecipazione pubblica STET, ora Telecom Italia, ed in particolare con la neonata società di servizi digitali STREAM SpA che anni dopo venne ceduta a Sky Italia. Il progetto in questione prevedeva la realizzazione di una piattaforma digitale di TV interattiva con flussi di dati digitali (per lo più film di prima visione e documentari) in streaming MPEG2 a 1,5 Mbps su doppino telefonico e l’installazione, presso i 300 utenti sperimentatori, di un innovativo set-top box ADSL prodotto da alcune società italiane ed in particolare da una prestigiosa azienda italiana, l’Italsiel del gruppo Italtel che purtroppo scomparve come la stessa STREAM nel rivolo delle successive privatizzazioni facendo perdere un know how aziendale inestimabile ed a vantaggio di capitali privati.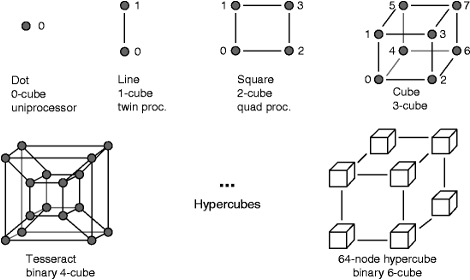 
In quegli anni, STREAM, in anteprima mondiale e battendo sul tempo gli stessi partners americani erogò per prima un servizio denominato VideoMagic di Video On Demand e PayTV su doppino telefonico. Le infrastrutture tecnologiche che costarono alle casse di STET oltre 10Mld di lire, furono predisposte presso la centrale telefonica di Lanciani a Roma e prevedevano un multiplexer sviluppato a partire da una matrice ipercubica all’interno di un supercalcolatore NCUBE a 512 processori (vedi schema in figura a 64-nodi, ovvero 8 cubi di 8 processori per un totale di 64 processori disposti ad ipercubo) che opportunamente programmata con tecniche di processazione parallela (array processor and parallel processing[B008]), fungeva da pumping machine per l’invio di flussi di dati MPEG2 a 1.5 Megabit per secondo.
Inoltre, con l’architettura logica dei processori NCUBE organizzati in strutture di interconnessione piramidale o a matrice ipercubica ed utilizzati come risorse di calcolo su viste vettoriali, era altresì possibile effettuare l’encoding massivo dei contenuti multimediali in standard mpeg2 (tipicamente film successivi alla prima visione), che venivano poi memorizzati con tecniche innovative di striping verticale e mirroring e successivamente indicizzati in una particolare Storage Area in alta affidabilità con totale parallelizzazione dei flussi di dati pronti per essere fruiti dagli utenti. 
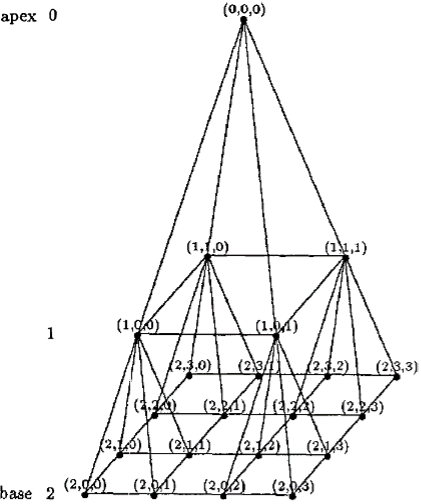Le stesse società americane che presero parte alla sperimentazione ovvero NCUBE e Bell Atlantic cui si aggiunse successivamente IBM, sono ora tra le principali collaboratrici del Dipartimento della Difesa americano per tramite del MIT (Massachusetts Institute of Technology) e della Lockheed Martin sui nuovi scenari di calcolo quantistico e di algoritmi di crittografia quantistica per il settore difesa che trassero spunti non indifferenti di ricerca applicata da quelle lontane esperienze italiane a cavallo tra gli anni ‘80 e ’90.
Il principio di Heisemberg[B006]
La fisica quantistica nasce dalla scoperta della doppia natura corpuscolare ed ondulatoria del fotone di luce. Un principio chiave alla base della fisica quantistica è il principio di indeterminazione di Heisenberg (a fianco in una foto del 1927). Questo principio sostiene che non è possibile conoscere, simultaneamente e con precisione assoluta, alcune particolari coppie di caratteristiche di un oggetto quantistico, ad esempio la posizione e la quantità di moto. Se si cerca di misurare esattamente la posizione di un elettrone, si perde la possibilità di verificarne la quantità di moto. Se, invece, si misura con precisione assoluta la quantità di moto, si perdono inevitabilmente informazioni sul luogo in cui l’elettrone si trova. Va inoltre sottolineato che queste sono limitazioni sempre valide anche se sussistono perturbazioni introdotte dall’apparato di misurazione. Secondo la meccanica quantistica questa soglia di indeterminazione non è concettualmente eliminabile.
Il computer quantistico[B003]
La computazione classica si basa sul modello della Macchina di Turing con il concetto classico di bit che può assumere i valori 0 o 1.
Definito nel 1936 dal matematico inglese Alan Turing e successivamente rielaborato da Von Neumann negli anni ’40, il modello di Macchina di Turing è alla base degli attuali sistemi di calcolo elettronico. Successivamente il fisico Feynman dimostrò che nessuna Macchina di Turing classica poteva simulare certi fenomeni fisici senza incorrere in un rallentamento esponenziale delle sue prestazioni. Al contrario, un “simulatore quantistico universale” avrebbe invece potuto effettuare i calcoli in maniera più efficiente. Nel 1985 Deutsch formalizzò queste idee nella sua Macchina di Turing Quantistica Universale.L’introduzione del nuovo modello di calcolo provocò degli effetti nel campo della complessità computazionale ed in particolare per i possibili scenari di rottura di chiavi di criptazione. Difatti nel 1994 il ricercatore Shor ebbe a dimostrare che il problema della fattorizzazione dei numeri primi si può ricondurre a tempistiche polinomiali per mezzo di un algoritmo quantistico. In un computer quantistico l’unità fondamentale di informazione è il quantum bit o qubit[B007]. Per spiegare questo concetto dobbiamo fare uso di una notazione matematica, conosciuta come notazione di Dirac. Per rappresentare lo stato di un qubit si utilizza un vettore unitario in uno spazio vettoriale complesso a due dimensioni. Come è noto lo stato di un bit classico viene descritto mediante i valori 0 ed 1, per il qubit invece la rappresentazione degli stati è fornita dalla formula:
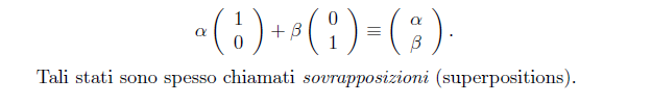
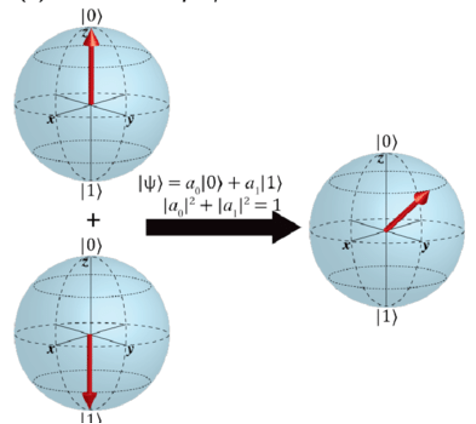
È possibile inoltre utilizzare la rappresentazione detta BRA KET della stessa formula ovvero:
∣ѱ〉 = α∣0〉 + β∣1〉
dove α e β sono numeri complessi tali che |α|²+|β|² = 1. Da ciò deduciamo che gli stati quantistici dipendono da valori di probabilità di α e β che si muovono de facto in una sfera geometrica, aprendo scenari interessanti per la risoluzione di problemi di crittografia ellittica come proposti da Neal Koblitz e Victor Miller e che possono essere descritti da equazioni in coordinate polari. 
Lo stato Iѱ> dell’equazione precedente può infatti essere riformulato secondo la normalizzazione di Bloch con tre parametri indipendenti dei quali e sono valori trascurabili mentre i parametri sono associati a punti di una sfera secondo le regole riportate in figura. Un’importante caratteristica distintiva tra qubit e bit classici è che due o più qubit possono manifestare un entanglement quantistico. L‘entanglement quantistico è una proprietà non locale di due o più qubit che consente ad un insieme di qubit di esprimere una correlazione maggiore di quella possibile nei sistemi classici. Una sorta di interconnessione superposizionale che lega un qubit ad uno o più qubit e che consente ad esempio di ottenere informazioni di un qubit agendo sul qubit correlato. Ciò viene mutuato in fisica quantistica dai movimenti di spin di due elettroni collegati. Circuiti quantistici che collegano i qubit, registri quantistici e porte logiche controllate ad esempio CNOT completano il modello di un computer quantistico.
Complessità computazionale
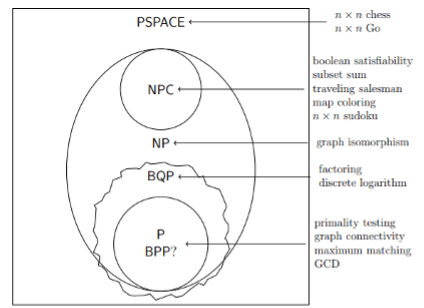Nella computazione classica abbiamo principalmente due classi di complessità temporale: la classe P (Polinomial) e quella NP (Non Polinomial o NPC Non Polinomial Completed ovvero un problema NP di difficile risoluzione, per esempio, quello del commesso viaggiatore). Nella prima si hanno tutti i problemi che si possono risolvere efficientemente, cioè mediante un algoritmo deterministico in tempo polinomiale, mentre la seconda comprende tutti quei problemi risolvibili da una macchina di Turing non-deterministica in tempo polinomiale. Un’altra importante classe di complessità è denotata con il nome PSPACE, dove si introduce la componente spaziale, ad esempio una scacchiera organizzata a matrice n x n dove muoversi all’interno. I risultati finora ottenuti in complessità computazionale stabiliscono la seguente relazione gerarchica: P <= NP <= PSPACE. Con l’introduzione degli algoritmi probabilistici è stata introdotta una nuova classe chiamata BPP (Bounded Polynomial Probabilistic). Questa classe comprende tutti quei problemi che si possono risolvere in tempi polinomiali (citiamo ad esempio il GCD Greatest Common Divisor) e con una probabilità di errore molto bassa. La teoria della complessità computazionale quantistica fa dunque riferimento al Modello della Macchina di Turing Quantistica. In questo contesto si è proceduto a definire la classe BQP che comprende tutti i problemi che si possono risolvere con una probabilità di errore piccola usando un circuito quantistico polinomiale. Il risultato ottenuto è il seguente: BPP<= BQP <= PSPACE
Crittografia quantistica
La crittografia quantistica offre qualcosa che non è possibile realizzare nel dominio classico. Permette di distribuire (o più precisamente, di generare casualmente) una chiave segreta su un canale di comunicazione aperto. Le leggi della fisica come le conosciamo oggi garantiscono che qualsiasi tentativo di intercettazione su questo canale aperto introdurrà errori nel chiave, e quindi l’intercettazione viene sicuramente rivelata. La crittografia quantistica non può trasmettere in modo sicuro un’informazione predeterminata; può generare in modo sicuro solo una chiave casuale. Una volta generata, questa chiave casuale può essere successivamente utilizzata in un cifrario simmetrico, come l’one-time pad o uno dei moderni cifrari simmetrici, per trasmettere dati in modo sicuro su un canale di comunicazione classico. Un canale di crittografia quantistica in esecuzione genererà costantemente nuovo materiale chiave segreto. Pertanto, la crittografia quantistica sta risolvendo il problema più difficile dei moderni crittografia, quella della distribuzione delle chiavi. La crittografia quantistica utilizza stati quantistici, come le polarizzazioni di singoli fotoni, trasmettere bit di informazione. Non è possibile fare una copia perfetta di uno sconosciuto stato quantistico [10], che preclude la sua misurazione precisa da parte di un intercettatore. Forse il lettore ricorderebbe il principio di indeterminazione di Heisenberg: se si misura la posizione precisa di una particella, tutte le informazioni sulla sua quantità di moto vengono perse e viceversa. Esistono molte coppie di proprietà che non possono essere misurate con precisione simultaneamente: per esempio, gli stati orizzontale-verticale e diagonale di polarizzazione dei fotoni sono una di queste coppie[B009].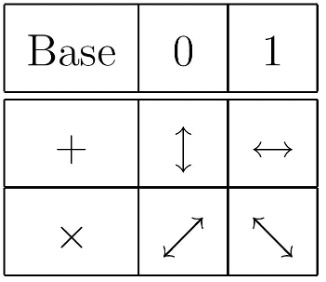
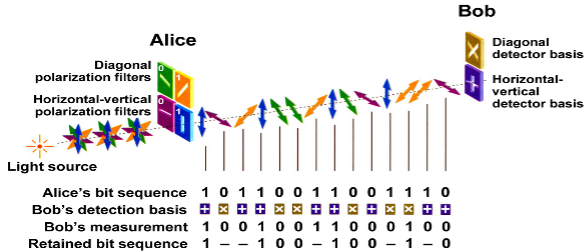
Un protocollo che permette lo scambio di una chiave tra due utenti e garantisce che questa non possa essere intercettata da terzi senza che i due se ne accorgano è chiamato BB84, dal nome dei suoi ideatori, Bennet e Brassard. Immaginiamo che Alice e Bob dispongano di un canale quantistico e di uno classico (quindi passibile di intercettazione) su cui scambiare dati. Sul canale quantistico Alice invierà fotoni con una determinata polarizzazione scelta a caso tra quattro possibili, ad esempio: 0°, 45°, 90°, 135°. Queste orientazioni determinano rispettivamente le basi: + e x non ortogonali tra di loro. Per ogni base, un’orientazione è interpretata come 0 e l’altra come 1. [B010]
Bob, ricevuti i fotoni dovrà effettuare una misura su di essi per scoprire con che polarizzazione sono stati spediti. Sarà quindi costretto a scegliere fra due diverse misure che, per il principio di indeterminazione di Heisenberg, non sono compatibili: con la prima può scoprire la polarizzazione dei fotoni se questi sono nella base +, con l’altra misura può scoprire la polarizzazione se i fotoni sono nella base x, in nessun caso è possibile ottenere queste due misure contemporaneamente. Se Bob sceglierà la misura sbagliata rispetto alla base usata da Alice, il risultato della misura sarà casuale, ovvero 0 oppure 1 con probabilità del 50%. Quindi anche un eventuale attaccante si troverebbe nella stessa situazione di Bob: infatti quando la spia intercetta i fotoni dovrà anch’essa scegliere tra le due misure possibili e se sceglie quella sbagliata ottiene un risultato casuale. Inviata una quantità sufficiente di fotoni, Bob invierà ad Alice pubblicamente le basi che ha utilizzato per le misurazioni, ma non cosa ha misurato ed Alice renderà note le basi che ha utilizzato per polarizzare i fotoni, ma non la polarizzazione degli stessi. I due potranno così scartare tutti i fotoni per i quali Bob ha scelto la base sbagliata. A questo punto Alice e Bob possederanno una chiave segreta comune ad entrambi valida per cifrare il messaggio. Per essere sicuri che la spia non abbia intercettato la chiave basta notare che se questa avesse in qualche modo intercettato i fotoni nel loro tragitto tra Alice e Bob, per il principio d’indeterminazione, ne avrà necessariamente modificato le caratteristiche introducendo quindi degli errori nella misura di Bob anche nei bit che dovrebbero risultare corretti. Quindi, se dopo aver scartato i bit, la chiave di Bob risulta diversa da quella di Alice, vuol dire che la spia ha intercettato i fotoni e che la chiave non è sicura.
Un secondo protocollo proposto da Artur Ekert nel 1991[B011], creato per consentire lo scambio di una chiave crittografica in modo sicuro tra due utenti, si basa sul principio fisico dell’entanglement quantistico. Questo algoritmo utilizza coppie di fotoni appunto entangled, cioè fotoni con particolari caratteristiche di correlazione. Supponiamo di avere una sorgente che emette con regolarità, ad esempio ogni secondo, una coppia di fotoni entangled che si propaghino in versi opposti, uno verso il mittente (Alice) e l’altro verso il destinatario (Bob). Supponiamo inoltre che lo stato della coppia dei fotoni sia dato dall’equazione seguente:
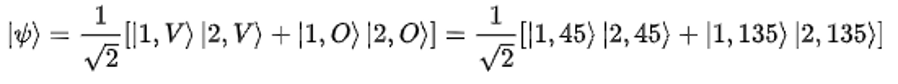
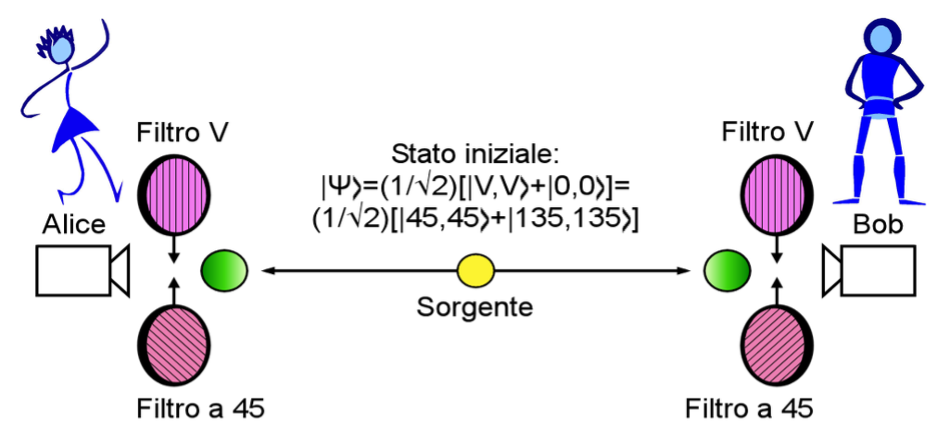Un sistema così preparato permette di ottenere dei fotoni nello stesso stato di spin cioè, se il primo ha una certa orientazione di spin anche il secondo dovrà avere necessariamente la stessa orientazione. Alice e Bob si dovranno essere precedentemente accordati di eseguire misure di polarizzazione lungo le due direzioni prescelte (appunto 0° e 45°), ma non sulla successione delle misure da eseguire. Ciascuno dei due sceglierà quindi in maniera perfettamente casuale la direzione lungo cui eseguire ciascuna misura individuale. Si può notare che la scelta delle due direzioni lungo cui verranno eseguite le misure può essere resa pubblica.
Tipologie di computer quantistici e simulatori
Nel prossimo futuro il computer quantistico sarà molto utilizzato per alcune casistiche risolutive dove la componente Non Polinomiale (NP) dello spazio delle soluzioni e quindi la natura probabilistica risulta una predominante. Citiamo alcuni di questi scenari: reti neurali ed intelligenza artificiale, chimica e biochimica, scenari di controllo dei domini della conflittualità (aria, acqua, terra, spazio e dominio cibernetico), settori finanziari e di trading, algoritmi predittivi, alte energie ed energie rinnovabili, biotecnologie e virologia, tecnologie dei materiali e nano tecnologie, simulazioni e test previsionali, cybersecurity, crittografia ed analisi malware.
Un computer quantistico è costituito da tre parti fondamentali:
- lo spazio di alloggiamento dei qubit
- un metodo per il trasferimento dei segnali ai qubit
- un computer per l’esecuzione di programmi tradizionali.
Le tecnologie usate per i qubit sono molto sensibile alle sollecitazioni ambientali. I segnali possono essere inviati ai qubit usando diversi metodi, tra cui microonde, laser e tensione elettrica. ll computer quantistico deve inoltre affrontare numerose problematiche, in primis la correzione degli errori, nonchè la scalabilità dei qubit con il relativo aumento della frequenza degli errori. A causa di queste limitazioni, la disponibilità di un PC quantistico per il mercato desktop è una ipotesi ancora lontana, tuttavia un computer quantistico per attività di laboratorio e di ricerca sarà una possibilità concreta[B005] dei prossimi anni. L’alloggiamento dei qubits verrà mantenuto ad una temperatura prossima allo zero assoluto attraverso raffreddamento ad elio o con altre soluzioni per massimizzarne lo stato di coerenza. Altri tipi di alloggiamento dei qubit usano una camera sottovuoto per ridurre le vibrazioni e stabilizzarli.
Nella foto il supercomputer quantistico Q di IBM.
Recentemente IBM ha mostrato un qubit superconduttore tridimensionale, sviluppato in collaborazione con Yale University. 
IBM ha usato un qubit di tipo 3D (Q1,Q2,Q3) per estendere fino a 100 microsecondi il periodo in cui il qubit mantiene i suoi stati quantistici coerenti. Questo valore supera la soglia minima necessaria per permettere schemi di correzione d’errore e permette agli scienziati di iniziare a focalizzarsi su aspetti ingegneristici di più ampia portata anche d tipo commerciale. Secondo analisti ed esperti del settore, soprattutto per applicazioni in campo militare, il miglior compromesso sarà la mappatura tra architetture di processori ipercubici con circuiti qubit quantistici a superconduttore e con risoluzione in tempistiche polinomiali di problemi NP riconducibili a scenari di mappatura ipercubica[B002]. Saremo quindi difronte ad una nuova generazione di computer ibridi che supereranno i limiti attuali imposti dalla legge di More con le sue limitazioni verso un nuovo orizzonte degli eventi più consono alle esigenze di coniugare i fenomeni naturali con la tecnologia e consentire all’uomo di raggiungere traguardi evolutivi di portata epocale.
Autore: Francesco Corona
Bibliografia Utile
[B001] https://www.semanticscholar.org/paper/Dilation-d-embedding-of-a-hyper-pyramid-into-a-Ho-Johnsson/ffe06b272ec19fb5eb976b5ee516c099a8965e36 [B002] https://innovationorigins.com/en/multidimensional-hypercube-quantum-physicists-discover-new-atomic-state/ [B003] Emma Strubel, Quantum Tutorial , Spring 2011 [B004] https://aimath.org/workshops/upcoming/hypercubequantum/ [B006] Principio di indeterminazione di Heisenberg – YouTube [B007] How Does a Quantum Computer Work? – YouTube [B008] Dan I. Moldovan Parallel Processing. From Application to Systems, Morgan Kaufmann, California 1993. [B009] Vadim Makarov, Quantum cryptography and quantum cryptanalysi, Trondheim, March 2007 [B010] Wikipedia crittografia quantistica[B011] https://youtu.be/LaLzshIosDk
